MD5 (Message Digest 5) は暗号学的ハッシュ関数で、電子署名やパスワードのハッシュ化のような暗号的な用途に利用されていた(が、今は暗号用途で使ってはいけない)。
暗号学的ハッシュ関数はこの性質を満たさなければいけないとされている。
- 一方向性: ハッシュ値から元の値の復元が困難である
- 第二現像困難性: あるハッシュ値があったとき、それと同じハッシュ値となる入力値(元の値でなくて良い)を求めるのが困難である
- 衝突困難性: 同じハッシュ値になる任意の入力値を求めることが困難である

ハッシュ関数の品質として通常利用時に偶然衝突する確率が非常に低いことはもちろん、悪意を持って衝突しようとしても偶然衝突するレベルの確率でしか成功しないようにする必要がある。ここでいう「困難」は総当たり攻撃や誕生日攻撃 1 よりも効率的な攻撃方法が無いと言い換えられる。
攻撃難易度は、 一方向性 > 第二現像困難性(弱衝突耐性) > 衝突困難性(強衝突耐性) の順番で、安全なハッシュ関数と言えるようにするためには、最低でも一番難易度が低い「衝突困難性(強衝突耐性)」ですら破れないことが求められる。
一方向性・第二現像困難性
この2つに関しては現時点は破られていない。なので直ちには電子署名を攻撃しメッセージの改ざんを検知できなくなるみたいな問題は起きない。
衝突困難性
既に破られている。
誕生日攻撃では 264 回の施行が必要になるが、2004年に 239 程度の試行で見つけられる方法が見つかり 2005年には 230 まで改善されたらしい(int 型より短いじゃん!)。
更に、2007年には chosen-prefix collition attack という前部分を任意の値にした状態で同一のハッシュを求めるような手法まで見つかっている。衝突を利用してX.509 証明書の偽装や、APOP を悪用すして31文字以下であれば現実的な時間でパスワードを盗めるような例もあったりする(詳しくは MD5の安全性の限界に関する調査研究報告書)。
実際に MD5 を衝突させてみる
HashClash というプロジェクトがある。これを使うことで画像のような md5 ハッシュ値が一致する入力のペアが作れる。
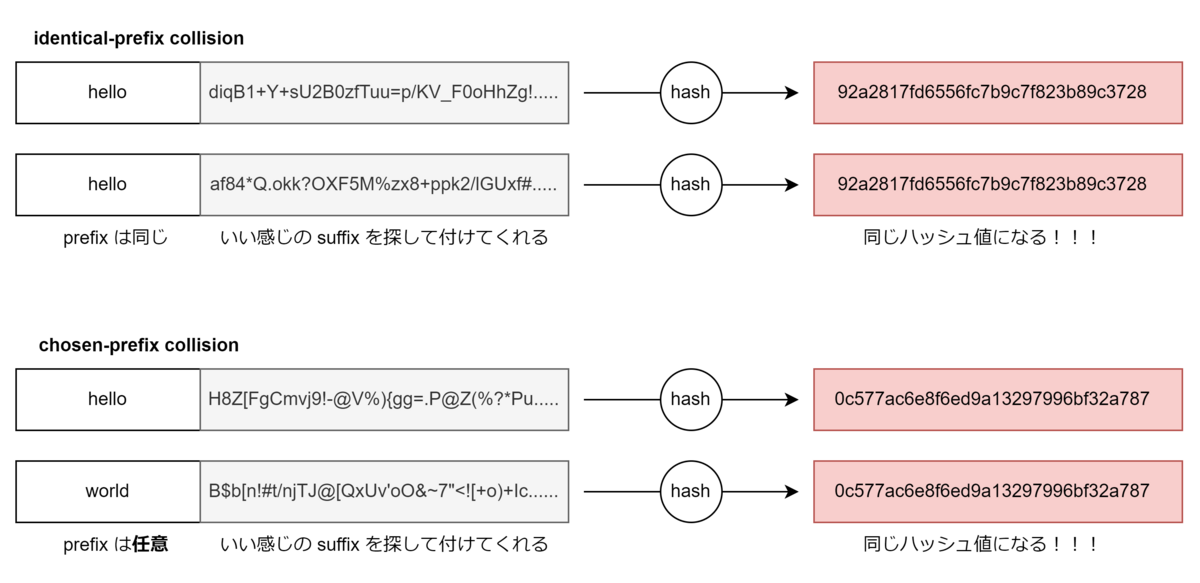
README に従ってビルドするか、releases からビルド済みのバイナリを入手できる。実際にこれを試してみる。
identical-prefix collision
プレフィックスをファイルに書き込み、準備されているスクリプトを実行する。2分半で collision1.bin collision2.bin が生成された。(一回目の実行では準備があるようでもう少しかかる)
$ echo -n hello > prefix $ ./scripts/poc_no.sh prefix
これはプレフィックスが同じだが(o どこ??)完全には一致しないバイナリファイルで
$ od collision1.bin -c 0000000 h e l l 327 023 254 025 - - 277 [ 277 373 215 266 0000020 x 311 356 302 l 327 247 7 | 373 322 e 216 % \f 373 0000040 o 320 Q Z Y E 225 326 033 265 s 272 204 d 272 O 0000060 317 / 265 037 \n 225 352 264 336 024 301 4 ; @ , < 0000100 : 267 2 323 307 333 253 333 \n 350 031 204 6 | 243 237 0000120 016 323 256 357 z 227 213 260 303 m 362 \f 0 \n j 340 0000140 016 377 l 351 \t ( 025 261 ^ 177 ; 005 % u r x 0000160 346 264 O j 215 004 321 317 001 e S @ 211 S 335 334 0000200 $ od collision2.bin -c 0000000 h e l l 327 023 254 025 - . 277 [ 277 373 215 266 0000020 x 311 356 302 l 327 247 7 | 373 322 e 216 % \f 373 0000040 o 320 Q Z Y E 225 326 033 265 s 272 204 d 272 O 0000060 317 / 265 037 \n 225 352 264 336 024 301 4 ; @ , < 0000100 : 267 2 323 307 333 253 333 \n 347 031 204 6 | 243 237 0000120 016 323 256 357 z 227 213 260 303 m 362 \f 0 \n j 340 0000140 016 377 l 351 \t ( 025 261 ^ 177 ; 005 % u r x 0000160 346 264 O j 215 004 321 317 001 e S @ 211 S 335 334 0000200 $ cmp collision1.bin collision2.bin collision1.bin collision2.bin 異なります: バイト 10、行 1
MD5 ハッシュが一致している!
$ md5sum collision1.bin 92a2817fd6556fc7b9c7f823b89c3728 collision1.bin $ md5sum collision2.bin 92a2817fd6556fc7b9c7f823b89c3728 collision2.bin
chosen-prefix collision
プレフィックスをファイルに書き込み、準備されているスクリプトを実行する。187分で prefix-1.coll prefix-2.coll が生成された。
$ echo -n hello > prefix-1 $ echo -n world > prefix-2 $ ./scripts/cpc.sh prefix-1 prefix-2
これは期待通り prefix が hello と world から始まるバイナリファイルで
$ od prefix-1.coll -c
0000000 h e l l o = b 204 021 001 u 323 M 353 200 223
0000020 336 1 301 331 0 E 373 276 036 q 360 \n c u 250 0
0000040 252 230 027 312 343 242 k 216 = D 251 217 362 016 g 226
0000060 H 227 % 246 \0 \0 \0 \0 9 206 377 323 % ] , 353
0000100 372 b U 247 246 305 312 034 260 k q u 201 210 ! 303
0000120 o u 025 270 a 213 211 257 367 021 253 k 8 l 206 {
0000140 ! 224 203 204 > 257 323 362 362 021 ) 341 X 202 270 352
0000160 325 347 335 t 355 M 026 0 201 | 246 021 354 ] 4 322
0000200 334 266 4 \b 265 321 346 210 377 [ 277 026 } 365 372 357
0000220 231 @ 204 250 035 D 373 006 256 271 251 212 353 / 327 324
0000240 232 u " 337 ] ~ 205 304 301 0 243 373 024 y 300 350
0000260 232 210 303 017 u s 324 { 333 321 224 324 262 \0 027 337
0000300 344 354 330 & 224 \t 307 037 002 r 351 & 240 " 311 324
0000320 034 024 355 . 304 001 356 > 361 F 370 * 017 A P H
0000340 316 3 a U y ! 7 ; 325 o \t q 6 242 036 327
0000360 - 0 353 d 301 221 347 226 @ N 2 334 354 + 200 S
0000400 032 345 352 350 247 = 022 025 U 250 \n 213 240 y 020 1
0000420 016 240 214 266 0 332 5 366 \b s 307 376 323 s 342 346
0000440 023 Z 372 K 361 177 256 237 243 ` 231 ~ ; 341 \b /
0000460 305 005 316 - 211 371 004 6 365 005 023 303 g V 2 301
0000500 o w J Q 377 220 360 # 232 303 337 373 340 034 277 `
0000520 D 030 317 264 302 z Q 372 336 327 o 334 } @ 025 021
0000540 < 342 344 244 N & G 342 < 333 } T 332 K 233 7
0000560 205 331 316 226 P 347 242 R 032 0 I 257 356 036 035
0000600 274 } 331 u { \t > 203 330 331 \v ? 377 G + 240
0000620 207 214 e 357 3 276 020 ( 026 \r 243 361 t 336 ` 235
0000640 315 344 227 334 0 ' 245 * X 256 244 333 276 ! 331 373
0000660 340 e 211 n 273 z 343 345 p 266 H \t 337 261 307 274
0000700 342 \0 265 266 K . 331 \v % 020 w 264 033 H 341 234
0000720 7 315 033 373 \f H 242 016 325 266 314 354 362 271 W t
0000740 201 370 d 340 313 211 374 207 347 F 275 021 363 L 221 372
0000760 350 216 241 ( s } 002 333 " 343 { 302 \t 004 < c
0001000
$ od prefix-2.coll -c
0000000 w o r l d 206 345 _ 320 203 001 233 M U 006 a
0000020 253 210 021 212 372 M 4 263 u Y F V 227 357 l J
0000040 \a 220 314 376 031 327 317 o 222 003 234 221 252 245 332 V
0000060 222 301 004 346 \0 \0 \0 \0 \b 213 205 375 275 211 262 307
0000100 372 b U 247 246 305 312 034 260 k q u 201 210 ! 303
0000120 o u 025 270 a 213 211 257 367 021 253 k 8 l 206 {
0000140 ! 224 203 204 > 257 323 362 362 021 ) 341 X 202 310 352
0000160 325 347 335 t 355 M 026 0 201 | 246 021 354 ] 4 322
0000200 334 266 4 \b 265 321 346 210 377 [ 277 026 } 365 372 357
0000220 231 @ 204 250 035 D 373 006 256 271 251 212 353 / 327 324
0000240 232 u " 337 ] ~ 205 304 301 0 243 373 024 231 300 350
0000260 232 210 303 017 u s 324 { 333 321 224 324 262 \0 027 337
0000300 344 354 330 & 224 \t 307 037 002 r 351 & 240 " 311 324
0000320 034 024 355 . 304 001 356 > 361 F 370 * 017 A P H
0000340 316 3 a U y ! 7 ; 325 o \t q 5 242 036 327
0000360 - 0 353 d 301 221 347 226 @ N 2 334 354 + 200 S
0000400 032 345 352 350 247 = 022 025 U 250 \n 213 240 y 020 1
0000420 016 240 214 266 0 332 5 366 \b s 307 376 323 s 342 346
0000440 023 Z 372 K 361 177 256 237 243 ` 231 ~ K 341 \b /
0000460 305 005 316 - 211 371 004 6 365 005 023 303 g V 2 301
0000500 o w J Q 377 220 360 # 232 303 337 373 340 034 277 `
0000520 D 030 317 264 302 z Q 372 336 327 o 334 } @ 025 021
0000540 < 342 344 244 N & G 342 < 333 } T 332 K 232 7
0000560 205 331 316 226 P 347 242 R 032 0 I 257 356 036 035
0000600 274 } 331 u { \t > 203 330 331 \v ? 377 G + 240
0000620 207 214 e 357 3 276 020 ( 026 \r 243 361 t 336 ` 235
0000640 315 344 227 334 0 ' 245 * X 256 244 333 276 # 331 373
0000660 340 e 211 n 273 z 343 345 p 266 H \t 337 261 307 274
0000700 342 \0 265 266 K . 331 \v % 020 w 264 033 H 341 234
0000720 7 315 033 373 \f H 242 016 325 266 314 354 362 271 W t
0000740 201 370 d 340 313 211 374 207 347 F 275 021 363 L 221 376
0000760 350 216 241 ( s } 002 333 " 343 { 302 \t 004 < c
0001000
MD5 ハッシュが一致している!!!
$ md5sum prefix-1.coll 0c577ac6e8f6ed9a13297996bf32a787 prefix-1.coll $ md5sum prefix-2.coll 0c577ac6e8f6ed9a13297996bf32a787 prefix-2.coll
まとめ
HashClash を利用して示したように、MD5 は一般的なPCでも数分~数時間あれば入力値の一部を任意の値にして衝突を発生させられることがわかった。(ちなみに最初はアルゴリズムを理解しようと論文を開いたが難しすぎて諦めた)
MD5 は一方向性・第二現像困難性が破られていないとはいえ衝突を悪用した攻撃方法は存在する。衝突困難性が破られてから20年以上経ってるので今後新しい悪用方法が現れる(どころか既に現れてる)ことは容易に想像できる。
ということで、MD5 やその他衝突困難性が破られているハッシュ関数(RIPEMD, SHA0, SHA1,... など)は暗号用途には使ってはいけない。
実験で作成した MD5 を衝突させたファイルはこちら
参考
- MD5 の場合出力が 128bit なので、第二現像困難性に対する総当り攻撃の平均試行回数は 2127 回、衝突困難性に対する誕生日攻撃の平均試行回数は 1.25 * √(2128) 回(≒ 264)程度↩
